Оценка точности триангуляции
К настоящему времени получено множество разных по форме и точности приближенных формул априорной оценки точности различных элементов геодезических сетей, создаваемых разными методами. Большинство из этих формул относится к схематическим геодезическим построениям, состоящим, например, из равносторонних треугольников, вытянутых ходов с одинаковыми длинами сторон и т. п. Тем не менее, как отмечалось выше, многие приближенные формулы до сих пор не потеряли своего значения и имеют важное методическое и практическое значение.
Поэтому воспользуемся некоторыми приближенными формулами для того, чтобы дать представление о точности построения государственной геодезической сети страны, сопоставить между собой по точности разные методы построения геодезических сетей, а также рассмотреть ряд других важных для производства вопросов.
Ряды
триангуляции 1 класса. Такие
ряды образуются из звеньев каждое длиной до 200 км. На обоих концах каждого звена измеряются базисные стороны b1, b2и определяются азимуты этих сторон ![]() и
и ![]() (рис. 37). Введем некоторые
обозначения, которыми будем пользоваться в дальнейшем: Si— связующие стороны (общие для смежных
треугольников);
(рис. 37). Введем некоторые
обозначения, которыми будем пользоваться в дальнейшем: Si— связующие стороны (общие для смежных
треугольников); ![]() — промежуточные стороны
треугольников;
— промежуточные стороны
треугольников; ![]() и Bi— связующие углы, лежащие против связующих
сторон; С — промежуточные углы; L— длина диагонали звена между его конечными пунктами.
и Bi— связующие углы, лежащие против связующих
сторон; С — промежуточные углы; L— длина диагонали звена между его конечными пунктами.
Пусть М — средняя квадратическая ошибка определения положения конечного пункта уравненного звена относительно его начального пункта. Ошибку М представим в виде суммы двух составляющих: mL— вдоль звена и mq— перпендикулярно к звену. В этом случае
![]() (5.29)
(5.29)
Ошибку ![]() принято
называть продольным сдвигом звена, а ошибку
принято
называть продольным сдвигом звена, а ошибку ![]() — поперечным
сдвигом.
— поперечным
сдвигом.
Допустим, что звено триангуляции с базисами и азимутами
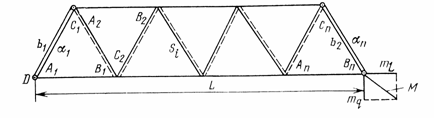
Рис. 37. Продольный и поперечный сдвиг звена триангуляции
на его концах состоит из равносторонних треугольников и уравнено по направлениям за условия фигур, базисов и азимутов. В таком звене средняя квадратическая ошибка логарифма связующей стороны (в единицах шестого знака логарифма) равна
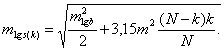 (5.30)
(5.30)
Относительную ошибку найдем по формуле
![]() (5.31)
(5.31)
Средняя квадратическая ошибка азимута связующей стороны, передаваемого по ходовой линии (показана пунктиром на рис. 37), равна
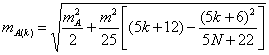 (5.32)
(5.32)
Продольный и поперечный сдвиги такого звена вычисляют по формулам:
![]()
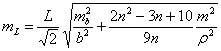 (5.33)
(5.33)
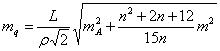 (5.34)
(5.34)
В формулах (5.30) — (5.34): N-— число треугольников в звене; k— номер треугольника, к которому относится оцениваемая сторона; п
— число промежуточных сторон в диагонали звена L = nS; m, ![]() ,
, ![]() — средние квадратические ошибки измерения
углов, азимутов Лапласа и базисных сторон соответственно. Ошибки логарифмов
базисных сторон
— средние квадратические ошибки измерения
углов, азимутов Лапласа и базисных сторон соответственно. Ошибки логарифмов
базисных сторон ![]() и связующих сторон
и связующих сторон ![]() выражены в единицах
шестого знака логарифма.
выражены в единицах
шестого знака логарифма.
Вычислим
по этим формулам средние квадратические ошибки элементов звена (см. рис. 37),
состоящего из равносторонних треугольников: в котором L=176 km, s = 22 km, N= = 16, я = 8, £ = 8, т = 0,7", ть1Ь=
1/400000 или ![]() ед. 6 знака lg;
ед. 6 знака lg; ![]() = 1,1".
= 1,1".
Средняя квадратическая ошибка связующей стороны в середине звена ms, м.............................0,13
Относительная ошибка ![]() ...............................................................................................................1/167
000
...............................................................................................................1/167
000
Средняя квадратическая ошибка азимута средней стороны звена А(к)………………………… 1,1”
Продольный сдвиг звена ![]() , м .........................................................................................................0,62
, м .........................................................................................................0,62
Поперечный сдвиг звена ![]() , м
..........................................................................................................0,76
, м
..........................................................................................................0,76
Общий сдвиг звена М,м ...........................................................................................0,98
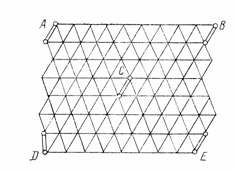
Рис. 38. Схема сплошной сети триангуляции 2 класса из равносторонних треугольников с измеренными азимутами и
базисными сторонами
Сплошные сети триангуляции. Вопросам оценки точности сплошных сетей триангуляции 2 класса, заполняющих полигоны триангуляции 1 класса размерами 200X200 км, посвящены обстоятельные исследования профессора А. И. Дурнева, профессора К. Л. Проворова, видных деятелей геодезического производства С. Г. Судакова, Д. А. Ларина и др. Наибольшее распространение получили формулы К. Л. Проворова, которыми мы и воспользуемся.
Приведенные ниже формулы (5.35) — (5.39) получены для сплошных сетей триангуляции 2 класса, состоящих из 100— 300 пунктов в каждой (рис. 38), уравненных как свободные по углам за условия фигур, горизонтов, полюсов, дирекционных углов и базисов, причем без учета ошибок исходных азимутов и базисов.
Исследования К. Л. Проворова показали, что между уравненными элементами в сплошной сети триангуляции 2 класса, состоящей из равносторонних треугольников, имеют место следующие простые соотношения
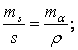
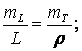 (5.35)
(5.35)
из которых следует, что
относительные ошибки сторон ![]() треугольников равны ошибкам
дирекционных углов этих сторон
треугольников равны ошибкам
дирекционных углов этих сторон ![]() , выраженным в
радианной мере. Это относится и к ошибкам диагоналей L, соединяющим несмежные пункты.
, выраженным в
радианной мере. Это относится и к ошибкам диагоналей L, соединяющим несмежные пункты.
Продольный сдвиг ![]() конца
любой диагонали Lотносительно ее начала равен поперечному
сдвигу и вычисляется по формуле
конца
любой диагонали Lотносительно ее начала равен поперечному
сдвигу и вычисляется по формуле
![]() (5.36)
(5.36)
где ошибка mT направления диагонали L равна
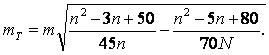 (5.37)
(5.37)
Здесь т — средняя квадратическая ошибки измерения углов; п — число треугольников в цепочке между конечными точками диагонали L; N — среднее число треугольников между базисными сторонами в сети. При n = N=24 и т=1,0" получим mL = mq = 0,44 м. Формула (5.37) справедлива при n ≤ N.
В сплошной сети триангуляции с треугольниками произвольной формы (с углами от 30 до 110°), уравненной по углам за все возникающие в ней геометрические условия:
средняя квадратическая ошибка дирекционного угла стороны в среднем равна
![]() (5.38)
(5.38)
средняя квадратическая ошибка логарифма стороны (в 6-ом знаке) будет
![]() (5.39)
(5.39)
где т — средняя
квадратическая ошибка измеренного угла; ![]() среднее число треугольников
между базисными сторонами в сети; параметр tвычисляется по формуле
среднее число треугольников
между базисными сторонами в сети; параметр tвычисляется по формуле
![]() (5.40)
(5.40)
или находится по аргументу N (табл. 9).
Формулы
(5.36) — (5.39) дают преуменьшенные значения средних квадратических ошибок,
поскольку не учитывают влияние ошибок измерения азимутов тА и
ошибок измерения базисных сторон ![]() -с учетом этого влияния
более точные значения ошибок та и
-с учетом этого влияния
более точные значения ошибок та и ![]() будут равна
будут равна
![]() (5.41)
(5.41)
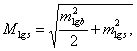 (5.42)
(5.42)
где та и ![]() вычисляются по формулам (5.38) и (5.39).
вычисляются по формулам (5.38) и (5.39).
Таблица 9
|
N |
t |
N |
t |
|
11 |
0,138 |
18 |
0,043 |
|
12 |
0,117 |
19 |
0,036 |
|
13 |
0,100 |
20 |
0,031 |
|
14 |
0,084 |
21 |
0,026 |
|
15 |
0,072 |
22 |
0,022 |
|
16 |
0,060 |
23 |
0,018 |
|
17 |
0,051 |
24 |
0,016 |
Допустим,
что в сплошной сети триангуляции базисные стороны с азимутами Лапласа на их
концах размещены в среднем через 24 треугольника (![]() = 24) горизонтальные углы и
азимуты измерены со средними квадратическими ошибками т =
= 24) горизонтальные углы и
азимуты измерены со средними квадратическими ошибками т = ![]() =
1,0"; базисные стороны измерены с ошибками
=
1,0"; базисные стороны измерены с ошибками ![]() = 1/300 000 или
= 1/300 000 или ![]() = l,45. При
= l,45. При ![]() = 24 параметр
= 24 параметр ![]() = 0,016 (см.
табл. 9).Используя эти данные, по формулам (5.41) и (5.42) получим:
= 0,016 (см.
табл. 9).Используя эти данные, по формулам (5.41) и (5.42) получим: ![]() = 1,0"
и
= 1,0"
и ![]() —2,1
ед. 6 знака логарифма или ms/s = = 1/200 000, что при длинах сторон
треугольников s = 7÷20 км приводит к ошибкам ms = 44÷10 см, т. е. в среднем
примерно 6 см. Такая точность построения опорной геодезической сети достаточна
для производства топографических съемок вплоть до масштаба 1:2000 и даже
более крупного (см. табл. 4).
—2,1
ед. 6 знака логарифма или ms/s = = 1/200 000, что при длинах сторон
треугольников s = 7÷20 км приводит к ошибкам ms = 44÷10 см, т. е. в среднем
примерно 6 см. Такая точность построения опорной геодезической сети достаточна
для производства топографических съемок вплоть до масштаба 1:2000 и даже
более крупного (см. табл. 4).
Частота размещения азимутов. Азимуты Лапласа играют важную роль при создании опорных геодезических сетей: обеспечивают независимую азимутальную ориентировку сторон геодезической сети во всех ее частях, причем с одинаковой высокой точностью; позволяют контролировать результаты угловых измерений по невязкам азимутальных условий, ослабляя при этом влияние систематических ошибок измерений; приводят к возникновению азимутальных условных уравнений при уравнивании сети и тем самым способствуют повышению ее точности.
Рассчитаем предельно
допустимое число треугольников ![]() , через которое необходимо
размещать азимуты Лапласа в триангуляции, чтобы они могли выполнять функцию
контроля угловых измерений.
, через которое необходимо
размещать азимуты Лапласа в триангуляции, чтобы они могли выполнять функцию
контроля угловых измерений.
Пусть на
концах цепочки треугольников (см. рис. 37) измерены азимуты ![]() и
и ![]() . Используя
промежуточные углы
. Используя
промежуточные углы ![]() треугольников, напишем
в общем случае
треугольников, напишем
в общем случае
![]()
Перейдя к средним квадратическим ошибкам, получим
2т2а = ![]()
где тα и т — средние квадратические ошибки измерения азимутов и углов соответственно; п — число промежуточных углов, равное числу треугольников между азимутами.
Пусть заданы
предельные значения ошибок: ![]() и
и ![]() . Тогда при заданном
значении средней квадратической ошибки т" измерения углов и
. Тогда при заданном
значении средней квадратической ошибки т" измерения углов и ![]() = 2,5, как
это принято в геодезии при расчете допусков, найдем
= 2,5, как
это принято в геодезии при расчете допусков, найдем
![]() (5.43)
(5.43)
При тα =т получим
![]() =12;
при тα = 1,0"и
=12;
при тα = 1,0"и ![]() = 0,7"—
= 0,7"—![]() = 25.
= 25.
Звенья триангуляции 1 класса состоят из 12—16 треугольников. В сетях триангуляции 2 класса в соответствии с требованиями инструкции азимуты должны определяться не более чем через 25 треугольников, что вполне согласуется с расчетом по формуле (5.43).
Частота размещения базисных сторон. Базисные стороны в триангуляции, как и азимуты Лапласа, играют важную роль. Они устанавливают единый масштаб построения геодезических сетей на земной поверхности; позволяют контролировать точность передачи длин сторон, ослабляя при этом накопление систематических ошибок измерений; приводят к возникновению базисных условных уравнений при уравнивании геодезической сети и тем самым способствуют повышению ее точности.
В целях обеспечения стройной системы построения государственной геодезической сети азимуты Лапласа принято определять на обоих концах базисных сторон. Поэтому в триангуляции частота размещения базисных сторон такая же, как азимутов Лапласа.
Выгоднейшая форма треугольников. В триангуляции любая сторона треугольника имеет одинаково важное значение, поэтому связующие s и промежуточные с стороны треугольников должны при прочих равных условиях определяться с одинаковой высокой точностью. Это требование может быть записано в виде равенства
![]()
При
реализации данного требования треугольники в рядах триангуляции получаются
равнобедренными с углами С=![]() = 52°46' и
= 52°46' и ![]() = 74°28'.
= 74°28'.
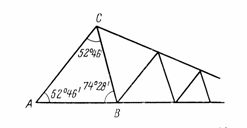
Рис. 39. Схема цепи треугольников с «выгоднейшими» углами
Однако такая форма треугольников не пригодна для практики, поскольку в этом случае ряд «вырождается» по мере удаления от исходной базисной стороны (рис. 39). С практической точки зрения наиболее выгодными по форме являются равносторонние треугольники, построение которых, однако, не всегда возможно вследствие особенностей рельефа местности. В рядах триангуляции 1 класса углы в треугольниках должны быть не менее 40°, а в сплошных сетях триангуляции 2 класса — не менее 30°.